Calculating Wire Twist Under Torque¶

For a cylinderical rod under torsion, the equation used to calculate the twist angle looks like this:

\[ \alpha = \frac{Q l}{J G} \]

Where;

\(\alpha\) is the twist angle in radians
\(Q\) is the torque (in lb)
\(J\) is the polar moment of inertia,
\(G\) is the shear (Young’s) modulus
\(l\) is the length of the rod
\(r\) is the radius of the rod

The equation for \(J\) for a rod with radius \(r\) is given by:

\[ J = \pi \frac{r^4}{2} \]

The shear modulus for music wire is about 11500000 \(\frac{lb}{in^2}\)

Let’s do some calculations and see what we get. We will use the Python pint library to check the units in our calculations:

import math
from pint import UnitRegistry
ureg = UnitRegistry()

Q = 0.4 * (ureg.inch * ureg.oz)
l = 12 * (ureg.inch)
r = 0.0075 * (ureg.inch)  # 0.015 music wire
J = math.pi * r**4 / 2
G = 11500000 * (ureg.lb/ureg.inch**2) * 16 * (ureg.oz/ureg.lb)
alpha = Q * l / ( J * G)

The value of \(\alpha\) is in radians, so we need to convert those to degrees to get our answer:

alpha_deg = alpha.to(ureg.degrees)
print(J, alpha, alpha_deg)

4.970097752749477e-09 inch ** 4 5.248781376041896 dimensionless 300.7330204340693 degree

pint is pretty handy for making sure all your engineering data is in the right form to feed into your equations.

Thhese numbers are about right for my indoor flying. A nice plan showing how to build one like this was produced by Cazar Banks can be found in the

Let’s plot the twist angle as a function of torque:

Q = 0.0 * (ureg.inch * ureg.oz)
xval = []
yval = []
for i in range(50):
    alpha_deg  = (Q * l / ( J * G)).to(ureg.degrees)
    xval.append(Q.magnitude)
    yval.append(alpha_deg.magnitude)
    Q = Q + 0.01 * (ureg.inch * ureg.oz)

Now, we can plot this data to see the results:

import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(xval, yval)
plt.grid()
plt.show()

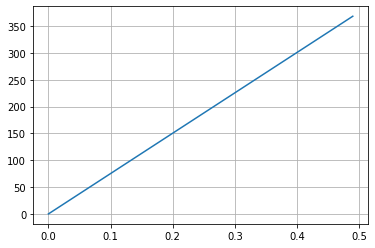
It looks like this code works. We can use this to set up a meter for our experiments.

Math Magic Aerodynamics

Calculating Wire Twist Under Torque¶